Synchronisation
A cooperating process is one that can affect or be affected by other processes executing in the system. Cooperating processes can either directly share a logical address space or be allowed to share data through shared memory or message passing. Concurrent access to shared data may result in data inconsistency.
A race condition occurs when several processes access and manipulate the same data concurrently and the outcome of the execution depends on the particular order in which the access takes place.
The Critical-Section Problem
Consider a system of \(n\) processes. Each proces has a segment of code, called the critical section, in which the process may be accessing - and updating - data that is shared with at least one other process. When one process is executing in its critical section, no other process is allowed to execute in its critical section. The critical-section problem is to design a protocol that the processes can use to synchronise their activity so as to cooperatively share data.
Each process must request permission to enter its critical section. The code implementing this request is the entry section. The critical section may be followed by an exit section. The remaining code is the remainder section.
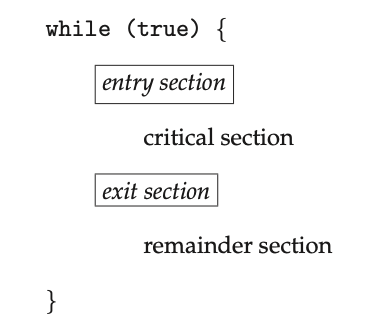
Figure: General structure of a typical process.
A solution to the critical-section problem must satisfy the following three requirements:
- Mutual exclusion: If process \(P_i\) is executing in its critical section, then no other process can be executing in their critical sections.
- Progress: If no process is executing in its critical section and some processes wish to enter their critical sections, then only those processes that are not executing in their remainder sections can participate in deciding which will enter its critical section next, and this selection cannot be postponed indefinitely.
- Bounded waiting: There exists a bound, or limit, on the number of times that other processes are allowed to enter their critical sections after a process has made a request to enter its critical section and before that request is granted.
There are two general approaches used to handle critical sections in operating systems:
- Preemptive kernels: A preemptive kernel allows a process to be preemped while it's running in kernel mode.
- Non-preemptive kernels: A non-preemptive kernel does not allow a process running in kernel mode to be preempted; A kernel-mode process will run until it exits kernel mode, blocks, or voluntarily yields control of the CPU.
A non-preemptive kernel is essentially free from race conditions on kernel data structures as only one process is active in the kernel at a time. Preemptive kernels on the other hand are not and must be carefully designed to ensure that shared kernel data is free from race conditions.
Despite this, preemptive kernels are still preferred as:
- They allow a real-time process to preempt a process currently running in kernel mode
- They are more responsive since there is less risk that a kernel-mode process will run for an arbitrarily long period before relinquishing the processor to waiting processes.
Peterson's Solution
Peterson's solution is a software-based solution to the critical-section problem. Due to how modern computer architectures perform basic machine-language instructions, there are no guarantees that Peterson's solution will work correctly on such architectures.
int turn;
boolean flag[2];
while (true) {
flag[i] = true;
turn = j;
while (flag[j] && turn == j);
// Critical section
flag[i] = false;
// Remainder section
}
Hardware Support for Synchronisation
Memory Barriers
How a computer architecture determines what memory guarantees it will provide to an application program is known as its memory model. A memory model falls into one of two categories:
- Strongly ordered: Where a memory modification on one processor is immediately visible to all other processors.
- Weakly ordered: Where modifications to memory on one processor may not be. immediately visible to other processors.
Memory models vary by processor type, so kernel developers cannot make assumptions regarding the visibility of modifications to memory on a shared-memory multiprocessor. To address this issue, computer architectures provide instructions that can force any changes in memory to be propagated to all other processors. Such instructions are know as memory barriers or memory fences.
When a memory barrier instruction is performed, the system ensures that all loads and stores are completed before any subsequent load or store operations are performed. This ensures that even if instructions were re-ordered, the store operations are completed in memory and visible to other processors before future load or store operations are performed.
Memory barriers are considered very low-level operations are are typically only used by kernel developers when writing specialised code that ensures mutual exclusion.
Hardware Instructions
Many computer systems provide special hardware instructions that allow us either
to test and modify the content of a word or to swap the contents of two words
atomically - that is, as one uninterruptible unit. These special instructions
can be used to solve the critical-section problem. Such examples of these instructions
are test_and_set() and
compare_and_swap.
boolean test_and_set(boolean *target) {
boolean rv = *target;
*target = true;
return rv;
}
Figure: The definition of the atomic test_and_set() instruction.
int compare_and_swap(int *value, int expected, int new_value) {
int temp = *value;
if (*value == expected) {
*value = new_value;
}
return temp;
}
Figure: The definition of the atomic compare_and_swap() instruction.
Atomic Variables
An atomic variable provides atomic operations on basic data types such as integers
and booleans. Most systems that support atomic variables provide special atomic
data types as well as functions for acessing and manipulating atomic variables.
These functions are often implemented using compare_and_swap() operations.
For example, the following increments the atomic integer sequence:
increment(&sequence);
where the increment() function is implemented using the CAS instruction:
void increment(atomic_int *v) {
int temp;
do {
temp = *v;
} while (temp != compare_and_swap(v, temp, temp + 1));
}
It's important to note however that although atomic variables provide atomic updates, they do not entirely solve race conditions in all circumstances.
Mutex Locks
Mutex, short for mutual exclusion, locks are used to protect critical sections and thus prevent race conditions. They act as high-level software tools to solve critical-section problems.
A process must first acquire a lock before entering a critical section; it then
releases the lock when it exits the critical section. The acquire() function
acquires the lock, and the release() function releases the lock. A mutex lock
has a boolean variable available whose value indicates if the lock is available
or not. Calls to either acquire() or release() must be performed atomically.
acquire() {
while (!available); /* busy wait */
available = false;;
}
release() {
available = true;
}
The type of mutex lock described above is also called a spin-lock due to the
process "spinning" while waiting for the lock to become available. The main
disadvantage with spin locks is that they require busy waiting. While a process
is in its critical section, any other process that tries to entir its critical
section must loop continuously in the call to acquire(). This wastes CPU cycles
that some other process might be able to use productively. On the other hand,
spinlocks do have an advantage in that no context switch is required when a process
must wait on a lock.
Semaphores
A semaphore \(S\) is an integer variable that, apart from initialisation, is
accessed only through two standard atomic operations: wait() and signal().
Operating systems often distinguish between counting and binary semaphores. The value of a counting semaphore can range over an unrestricted domain. The value of a binary semaphore can range only between 0 and 1.
Counting semaphores can be used to control access to a given resource consisting
of a finite number of instances. The semaphore is initialised to a number of
resources available. Each process that wishes to use a resource performs a wait()
operation on the semaphore (decrementing the count). When a process releases
resource, it performs a signal() operation (incrementing the count). When the
count for the semaphore goes to 0, all resources are being used. Processes wishing
to use a resource will block until the count becomes greater than 0.
wait(S) {
while (S <= 0); // busy wait
S--;
}
signal (S) {
S++;
}
Figure: Semaphore with busy waiting.
It's important to note that some definitions of the wait() and signal()
semaphore operations, like the example above, present the same problem that
spinlocks do, busy waiting. To overcome this, other definition of these functions
are modified as to when a process executes wait(), it suspends itself rather
than busy waiting. Suspending the process puts it back a waiting queue associated
with the semaphore. Control is then transferred to the CPU scheduler, which selects
another process to execute. A process that is suspended, waiting on a semaphore
\(S\), should be restarted when some other process executes a signal() operation.
A process that is suspended can be restarted by a wakeup() operation which
changes the process from the waiting state to the ready state subsequently placing
it into the ready queue.
typedef struct{
int value;
struct process *list;
} semaphore;
wait(semaphore *S) {
S->value--;
if (S->value < 0) {
add this process to S->list;
block();
}
}
signal(semaphore *S) {
S->value++;
if (S->value <= 0) {
remove a process P from S->list;
wakeup(P);
}
}
Figure: Semaphore without busy waiting.
Monitors
An abstract data type - or ADT - encapsulates data with a set of functions to operate on that data that are independent of any specific implementation of the ADT. A monitor type is an ADT that includes a set of programmer-defined operations that are provided with mutual exclusion within the monitor. The monitor type also declares the variables whose values define the state of an instance of that type, along with the bodies of functions that operate on those variables.
The representation of a monitor type cannot be used directly by the various processes. Thus, a function defined within a monitor can access only those variables declared locally within the monitor and its formal parameters. Similarly, the local variables of a monitor can be accessed by only the local functions.
The monitor construct ensures that only one process at a time is active within
the monitor. Consequently, the programmer does not need to code this synchronization
constraint explicitly. In some instances however, we need to define additional
synchronization mechanisms. These mechanisms are provided by the condition
construct. A programmer who needs to write a tailor-made synchronization scheme
can define one or more variables of type condition. The only operations that can
be invoked on a condition variable are wait() and signal().
The wait() means that the process invoking this operation is suspended until
another process invokes whereas the signal() operation resumes exactly one
suspended process. If no process is suspended, then the signal() operation has
no effect. Contrast this operation with the signal() operation associated with
semaphores, which always affects the state of the semaphore.
Now suppose that, when the x.signal() operation is invoked by a process \(P\),
there exists a suspended process \(Q\) associated with condition x. Clearly,
if the suspended process \(Q\) is allowed to resume its execution, the signaling
process \(P\) must wait. Otherwise, both \(P\) and \(Q\) would be active
simultaneously within the monitor. Two possibilities exist:
- Signal and wait: \(P\) either waits until \(Q\) leaves the monitor or waits for another condition.
- Signal and continue: \(Q\) either waits until \(P\) leaves the monitor or waits for another condition.
Liveness
Liveness refers to a set of properties that a system must satisfy to ensure that processes make progress during their execution life cycle. A process waiting indefinitely is an example of a "liveness failure". There are many different forms of liveness failure; however, all are generally characterised by poor performance and responsiveness.
Deadlock
The implementation of a semaphore with a waiting queue may result in a situation where two or more processes are waiting indefinitely for an event that can be caused only by one of the waiting processes. When such a state is reached, these processes are said to be deadlocked.
Priority Inversion
A scheduling challenge arises when a higher-priority process needs to read or modify kernel data that are currently being accessed by a lower-priority process — or a chain of lower-priority processes. Since kernel data are typically protected with a lock, the higher-priority process will have to wait for a lower-priority one to finish with the resource. The situation becomes more complicated if the lower-priority process is preempted in favor of another process with a higher priority.
This liveness problem is known as priority inversion, and it can occur only in systems with more than two priorities. Typically, priority inversion is avoided by implementing a priority-inheritance protocol. According to this protocol, all processes that are accessing resources needed by a higher-priority process inherit the higher priority until they are finished with the resources in question. When they are finished, their priorities revert to their original values.